[금융 머신러닝] 금융 데이터의 종류와 특성(1)

이번 글에서는 투자와 관련한 금융 데이터의 종류에는 무엇이 있는지, 또 데이터가 가진 특성에는 무엇이 있는지에 대해 써보려고 한다.

투자는 왜 어려울까

투자가 왜 어려운지를 생각해보면 투자 관련 금융 데이터에 대해 좀 더 쉽게 이해할 수 있다.

투자는 왜 어려울까? 세상에는 수많은 과학 이론이 있고 수없이 많은 사람들이 투자에 뛰어드는데 왜 아직도 언제든 통하는 완벽한 투자 이론이 없을까? 왜 그 대단한 뉴턴과 아인슈타인까지도 투자에 실패했을까?

그럼 반대로 사람들이 너무 잘 하는 과제에 대해 생각해보자. 개와 고양이 사진을 가져와서 어떤 사진이 개고 어떤 사진이 고양이인지 판단하는 문제는 사람에게는 누워서 떡 먹기다. 그럼 왜 이게 쉬운 문제인지 한 번 낯설게 바라보자. 어떤 부분 때문에 이 문제가 주식이 내일 상승할지 하락할지 판단하는 문제와 다를까?

Low signal-to-noise ratio

첫번째로는 잡음 대비 정보량이다. signal-to-noise ratio라고도 한다. 수천 장의 사진에서 고양이 사진을 골라내야 한다고 해보자. 거의 100%에 가깝게 구분할 수 있을 것이다. 흐리게 나온 사진이나 이상하게 생긴 개를 착각하는 경우에나 틀리게 된다. 이렇듯 높은 성공률이 high signal-to-noise ratio라는 것을 시사한다. 사진 내에서 고양이의 모습이 바로 문제를 푸는 데 필요한 정보량인 signal이고 흐린 얼룩이나 배경 이미지 등이 잡음, noise이다.

그러나 금융 데이터는 low signal-to-noise ratio를 가진다. 그 이유로는 먼저 금융 시장 자체가 noisy한 측면이(연간 변동성이 연간 수익률의 10배나 된다던지) 있다. 그리고 돈을 벌 수 있는 signal이 발견되면 시장 참여자들이 다같이 달려드는 통에 signal이 예측력을 잃어버리고 오히려 그 signal에 달려든 사람들의 이후 행동들 때문에 noise가 발생하기도 한다. 이러한 이유 등으로 인해 금융 데이터는 low signal-to-noise ratio라는 특성을 가진다.(Israel et al., 2020)

데이터가 low signal-to-noise ratio일 경우 큰 단점이 있다. 바로 training set에서 의미 있는 정보가 아닌 noise를 학습할 가능성이 높아진다는 것이다. 다시 말해 overfitting이 될 가능성이 높다는 뜻이다. 금융 데이터를 활용하여 머신러닝을 진행하는 경우 이 점을 유의해야 한다.

i.i.d (Independent and identically distributed)

두번째로는 데이터를 뽑아내는 상황이다. 개와 고양이 사진이 만들어진 상황에 대해 생각해보자. 개와 고양이의 모습은 언제나 동일하다. 개와 고양이 사진을 언제 찍어도, 개와 고양이의 모습은 변하지 않는다. 약간의 크기와 털 색깔이 다르다고는 해도, 개는 개만의 생김새를 가지고 있고 고양이는 고양이만의 생김새를 가지고 있다. 그렇기 때문에 개와 고양이라는 존재 자체를 모르던 아주 어린 아기도 개와 고양이를 반복적으로 보면 곧 이 둘을 구분할 수 있게 된다. 이를 다시 정리해서 말하자면 개와 고양이는 외모라는 관찰 가능한 변수에 있어서 독립적이고(하나의 확률변수가 다른 변수의 확률에 영향을 받지 않고) 동일한(표본과 모집단이 같은) 분포를 가지고 있다. 그래서 분포 내에서 training set, test set을 랜덤하게 샘플링한다고 했을 때 그 둘은 같은 분포에서 나왔다는 것을 보장할 수 있다.

그러나 주식의 등락 여부 경우는 어떨까? 만약 내일 주식의 등락 여부를 알기 위해 과거의 주가의 등락 데이터만 활용한다고 해보자. 10일간 매일 1%씩 짝수날은 올랐다가 홀수날은 내렸다가를 반복한 주식 A가 있다. 이 A는 11일째 되는 날에 5% 상승했다. 그런데 어제까지 이런 똑같은 등락을 반복한 주식 B가 있다고 했을 때 이 주식이 과연 내일 똑같이 상승할까? 이 문제의 경우에는 우리가 개와 고양이의 사진을 보고 판단하던 상황과는 달리 확신을 가질 수 없다.

왜 그럴까? 흔히들 시장은 변화하는 존재라고 말한다. 그 이유는 바로 금융 시장에 수많은 시장 참여자가 있고, 이 시장 참여자들은 수없이 바뀌고 서로에게 영향을 주며 관찰 가능한 데이터의 분포를 변화시키기 때문이다. 과거 어느 시점까지 모은 데이터의 분포가, 미래 데이터의 분포와 달라질 수 있는 것이다. 특히 외형적으로는 비슷해보이는 분포라도 우리가 알고 싶은 정보의 측면에 있어서는 다른 분포가 형성되어 있을 수 있다.

머신러닝 이론은 몇 가지 통계적인 가정을 기반으로 만들어졌다. 그 중 하나가 i.i.d(Independent and identically distributed) 가정이다. 어떤 패턴, 즉 어떤 확률분포를 학습하기 위해서는 그 분포에서 뽑아낸 training set과 test set이 독립적이고 동일한 분포에서 샘플링되어야 한다. 그렇지 않으면 training set의 분포를 열심히 학습시켜놨는데 test set은 정작 다른 분포를 가지고 있는 안타까운 상황이 펼쳐져 버린다. Overfitting이 되어버린 것이다. 원래 잘 되는 방법론에 overfitting을 방지할 수 있는 cross-validation 기법을 적용했어도 i.i.d 가정에 맞춘 제대로 된 training set, test set 샘플링이 이루어지지 않았으면 overfitting이 발생한다.

그래서 금융 머신러닝에서 중요한 것은 (1) 적절한 전처리를 하거나, (2) 예측하고자 하는 정보를 충분히 설명할 수 있는 변수들을 확보하여 샘플링할 대상의 분포를 정보 측면에서 i.i.d에 가깝게 만드는 것이다. 그래서 training set과 test set(그리고 향후 미래의 dataset까지) 샘플링을 잘 할 수 있게 해야 한다. 시장 참여자가 달라지고 시장 자체가 달라지기 때문에 완벽한 i.i.d를 만드는 것이 어려울 수도 있지만, 단기간 내에 변하지 않는 정보도 분명 존재한다. 자신만의 투자 전략을 개발해 높은 수익을 올린 투자 대가들의 존재가 이를 뒷받침한다. 그들의 머릿속에서 이루어진 전략 생성 과정이 바로 우리가 찾던 전처리와 변수 확보 방법이라 할 수 있겠다.

길게 썼지만 3줄 요약을 하자면 다음과 같다.

• 금융 데이터는 low signal-to-noise ratio를 가진다.
• 그리고 금융 시장은 변화하기 때문에 대다수의 관찰 가능한 금융 데이터가 i.i.d를 만족하지 않는다.
• 그래서 금융에 머신러닝을 잘 적용하려면 전처리나 feature 확보를 통해 signal-to-noise ratio를 높이고 정보 측면에 있어 i.i.d에 가까운 분포를 만들어야 한다.

금융 데이터의 종류

그럼 이제 금융 데이터에 뭐가 있는지, 각 데이터의 특성은 무엇인지 개인적으로 공부하면서 파악한 내용을 간략하게 서술하겠다.

여기 나와 있는 데이터가 전부는 아니고, 앞으로 공부를 하면서 추가할 것이 있다면 추가로 업데이트 하는 식으로 글을 관리하려고 한다.

금융 데이터는 (1) ‘데이터가 생성된 과정’에 따라 살펴볼 수도 있고, (2) 거래하고자 하는 ‘상품’에 따라 살펴볼 수도 있다. (2)까지 포함하면 글이 너무 길어질 것 같아서 별도의 글로 작성할 예정.

금융 데이터의 종류(1) 생성 과정에 따른 분류

금융 데이터는 생성 과정에 따라 크게 4가지 종류로 나뉜다.

• Fundamental data
• Market data
• Analytics
• Alternative data

Fundamental data

Fundamental data는 공시나 감독 기관에 제출하는 자료, 거시경제 데이터 등에 해당한다. 주로 분기별 재무제표 데이터가 여기 해당한다. 자산, 부채, 매출, 비용 및 이익 등의 데이터가 존재한다. Fundamental data는 주로 투자하고자 하는 대상에 대한 정보를 알 수 있다. 그리고 분기 단위로 존재하기 때문에 데이터의 빈도, 즉 데이터의 양이 매우 적은 편이다.

이 데이터를 다룰 때 유의해야 할 점은 데이터가 공개된 시점과 데이터가 설명하는 대상의 시점이 다르다는 것이다. 예를 들면 3분기 재무제표 공시가 이루어지면, 데이터는 7월부터 9월까지의 재무 상태에 대해서 다룬다. 그런데 이 데이터의 공시가 이루어진 날짜는 10월 말~11월 초다. 시간이 지난 뒤 Fundamental data를 활용해 분석을 하려고 할 때, 해당 정보를 회기 마지막 날인 9월 30일에 알게 되었다는 식으로 분석을 하면 문제가 생긴다. 시장에 정보가 공개되어 반영되는 시점은 공시되는 시점인데 그 전에 이미 정보를 알고 투자하는 전략을 만들게 된다.

또 Backfilling이나 수정값(reinstated value)에 대해서도 유의해야 한다. Backfilling은 당시에는 값을 몰랐음에도 데이터가 들어가 있는 상황을 말하고, 수정값은 처음 발표 이후에 값이 수정된 경우를 말한다. 위에서 살펴본 상황과 마찬가지로 수정된 값은 첫 발표 때는 알 수 없으므로 이를 유의하여 작업해야 한다.

따라서 Fundamental data를 제대로 활용하기 위해서는 해당 데이터가 실제 시장에 공개된 시점을 알아야 한다. 해당 시점까지 기록한 데이터는 Point-In-Time(PIT) data라 한다. 반면 공개된 시점이 아닌 회기를 기준으로 기록한 데이터는 lagged Non-PIT data라 한다. 두 데이터로 백테스트를 해보면 상당히 다른 결과를 보게 된다.(Breitschwerdt, 2015)

Market data

시장 데이터는 가격, 수익률, 변동성, 거래량, 배당/쿠폰, 시중 금리, 호가 데이터 등 거래소와 같은 시장에서 생성되는 데이터를 의미한다. 시장 참여자들에 대한 정보를 얻기 좋다. 그리고 Fundamental data와 달리 생성되는 데이터가 정말 많다.

시장 데이터는 기록하는 시간에 따라 Time resolution과 Time horizon라는 개념을 가지고 있다. Time resolution은 얼마나 dense하게 데이터를 기록하는지(월→주→일→시간→분→초→틱), Time horizon은 얼마만큼의 기간 동안 데이터를 기록할 것인지를 말하는 단위다. Time resolution은 정규화된 형식의 데이터인 Bar와도 관련이 있는데, 이것은 데이터 전처리 부분에서 더 자세히 다루면 좋을 것 같다.

미국에서는 FIX(Financial Information eXchange ) protocol이라는 것이 있어서 해당 데이터를 확보할 수만 있다면 당시의 시장 상황을 그대로 재구성해볼 수도 있는 것 같다. 단 하루에 만들어지는 데이터의 크기만 10TB라 하니.. 다루기는 쉽지 않을 것 같긴 하다.

호가 데이터는 시장미시구조 파악이나 HFT(High Frequency Trading)를 하는 데 있어 꼭 필요한 데이터다. HFT도 궁금하지만 이쪽은 아직 공부해보지 않은 분야라 추후 공부하고 기록하는 것으로 하자.

수익률 데이터

금융 머신러닝에서 가장 흔하게 쓰이는 데이터라 하면 바로 수익률 데이터다. 그 이유는 다음과 같다.

주가 데이터는 기본적으로는 비정상성을 가지고 있다. 정상성이란 시간이 흘러도 데이터의 통계적 성질이 유지되는 경우에 해당하는데, 평균, 분산, 공분산이 time-invariant해야 정상성을 가지고 있다고 한다.(엄격한 수학적 정의는 여기에 따로 쓰지는 않겠다) 주가 데이터는 이러한 조건을 만족시키지 않기 때문에 비정상성이다. 문제는 많은 통계 분석 방법이 데이터의 정상성을 가정하고 있다는 것이다.

그래서 보통 정상성을 확보하기 위해 대신 주가 데이터의 차분값인 주가수익률을 가지고 분석을 진행한다. 주가를 미분한 결과인 주가수익률은 정상성을 따른다고 알려져 있다. 덧붙이자면 일반적인 정수계 미분은 과거 주가에 대한 기억(memory)을 완전히 지워버리기 때문에, 분수계 미분을 통해 과거 기억을 보존하면서 정상성을 확보할 수 있는 방법을 사용하는 것이 정보 보존의 측면에서 좋다.(Prado, 2018) 분수계 미분을 통한 정상성 확보에 대한 자세한 내용은 추후 데이터 전처리와 관련한 별도의 글에서 정리할 예정이다. 오늘 글에서는 정수계 미분 기반의 수익률 데이터가 가지는 특성을 우선 다룬다.

또 주가수익률은 전략의 이익을 계산, 학습하기 위해 꼭 필요한 데이터이기도 하다. 그 때문인지는 몰라도 주가수익률 데이터의 특성에 대한 연구가 많이 이루어진 편이다.

Arithmetic return vs. Geometric return

수익률을 구할 수 있는 방법으로는 arithmetic return과 geometric return(로그 수익률이라고도 한다)이 있다.

Arithmetic return은 다음과 같이 구한다.

\[r_t = (Y_t - Y_{t-1})/Y_{t-1}\]

연속된 시점 t=0부터 t=T까지의 수익률을 구하려고 하면, arithmetic return은 다음과 같이 계산한다.

\[R = \frac{Y_T}{Y_{0}} - 1 = \frac{Y_T}{Y_{T-1}}\frac{Y_{T-1}}{Y_{T-2}}...\frac{Y_1}{Y_0} - 1 = \prod_{t=1}^{T} \frac{Y_t}{Y_{t-1}} - 1\]

한편 geometric return은 다음과 같이 구한다.

\[d_t = log(Y_t) - log(Y_{t-1})\]

연속된 시점 t=0부터 t=T까지의 수익률을 구하려고 하면, geometric return은 다음과 같이 계산한다.

\[D = log(\prod_{t=1}^{T} \frac{Y_t}{Y_{t-1}}) = \sum_{t=1}^{T}log(\frac{Y_t}{Y_{t-1}}) = \sum_{t=1}^{T}d_t\]

따라서 arithmetic return과 geometric return 사이의 관계는 \(D = log(1+R)\) 관계가 존재한다.

arithmetic return이 작으면 큰 차이가 나지 않지만, 다시 말해 변동성이 작고 time resolution이 높으면 큰 차이가 없지만, 변동성이 크고 time resolution이 작을수록 차이가 커진다. 아래 그래프에서는 특정 기간 동안 Norway는 44%, US는 18%의 annual volatility를 가진 상황에서의 arithmetic, geometric return 간 관계를 확인할 수 있다. 변동성이 큰 Norway에서 두 return의 차이가 보다 큰 것을 확인할 수 있다.(K Aas, 2004)

보통 geometric return이 time resolution에 무관하게 정규분포를 따른다고 가정한다. 그 유명한 Black & Scholes (Black and Scholes, 1973) 옵션 가격 모형도 이러한 가정을 기반으로 만들어졌다. 만약 geometric return이 정규분포를 따른다면, arithmetic return은 lognormal 분포를 따른다.(위에서 쓴 arithmetic return과 geometric return 사이의 관계 때문)

Heavy-tailed

위에서 보통 geometric return이 정규분포를 따른다는 가정을 한다고 했다. 그러나 실제로 geometric return 데이터를 살펴보면 time resolution이 dense할수록(월→주→일→시간→분→초) 분포가 heavy-tailed 특성을 가지게 된다. 반면 time horizon이 길수록 작은 엇나감들이 평균치로 사라지게 되면서 분포가 normal에 더 가깝게 된다. (Bradley and Taqqu, 2003)

수익률 데이터의 heavy-tailed 특성은 다음과 같은 단점을 가진다. Least squares 목적함수의 convexity 상에서 outlier가 존재할 경우 large error가 되어 큰 영향을 주기 때문에 OLS(Ordinary least squares) 기반 예측의 안정성이 낮아지게 된다.(Gu et al., 2018) 통계학계에서는 이런 문제를 해결하기 위해 outlier들의 존재에도 보다 안정적인 예측을 할 수 있도록 modified least squares 목적함수를 개발하였다. (Box, 1953, Tukey, 1960, Huber, 1964) 머신러닝 학계에서 주로 heavy-tailed 관측치의 단점에 대응하기 위한 방법은 Huber loss이다. 다음과 같이 일정한 범위 ξ 내에 있으면 least square를 하고, 그 밖에 있으면 오차의 절대값을 구하는 식이다. 파라미터 ξ는 데이터에 따라 달라질 수 있다.

Volatility clustering

짧은 기간 단위의 수익률 데이터는 서로 uncorrelated한 특성을 가지지만, independent하지는 않다. 좀 더 자세히 얘기하자면 연속된 가격 변화 움직임 자체는 independent하게 보일지라도, 그 절대값(absolute vlue) 또는 증감된 가격 데이터의 제곱(square of the price increments)으로 측정되는 magnitude(규모)가 시간에 따라 correlated된다.

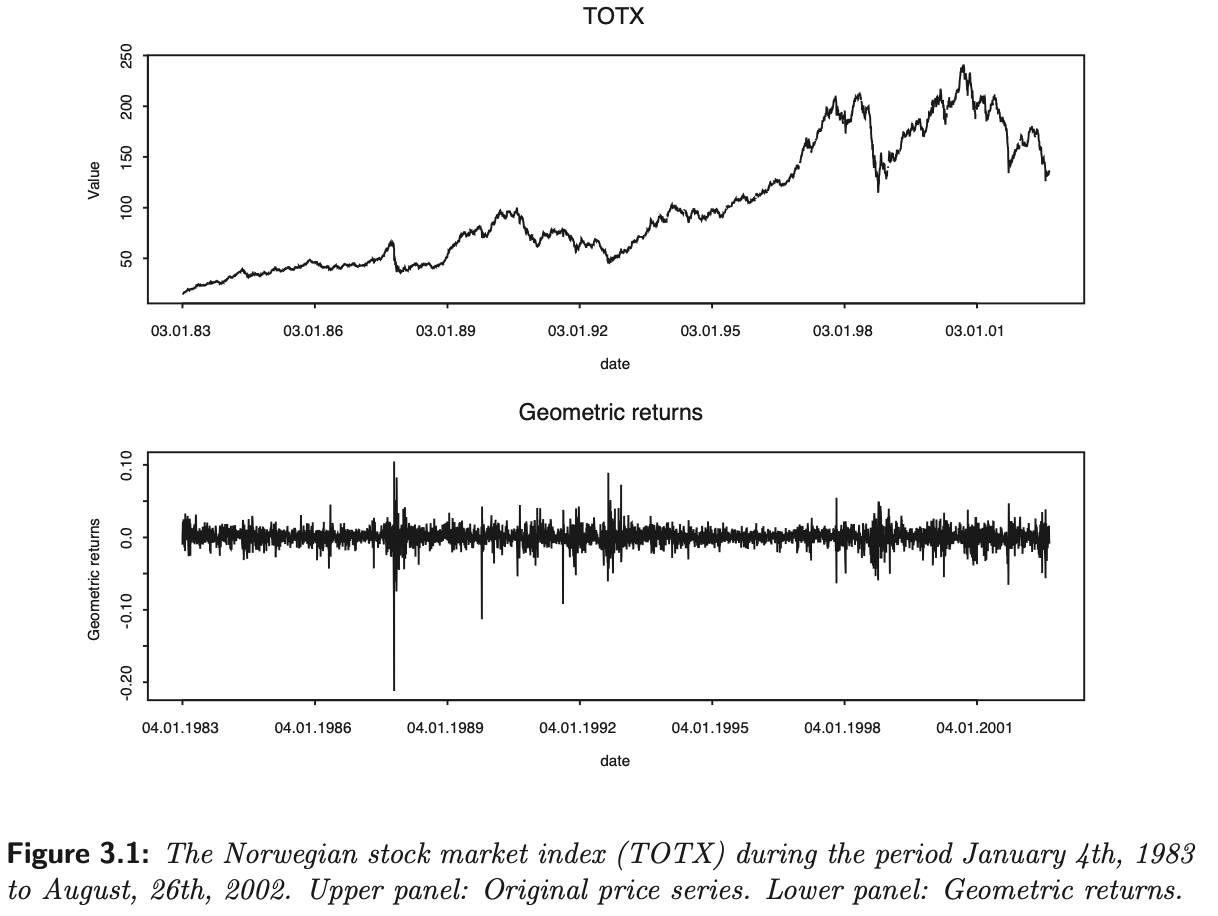
이러한 현상을 volatility clustering이라 부른다. 작은 가격 변동 뒤에는 작은 가격 변동들이 따르는 경향이 있고, 큰 가격 변동 뒤에는 큰 가격 변동이 따르는 경향이 있다. (Mandelbrot, 1963) 그래서 이러한 time-varying volatility를 설명하기 위한 금융 시계열 데이터 모델링으로 GARCH와 stochastic volatility model들이 사용된다.

Analytics

분석 데이터는 다른 데이터(Fundamental, market, alternative, 심지어는 다른 analytics data를 포함)를 기반으로 분석을 통해 만들어진 새로운 데이터다. 애널리스트의 추천 정보나 신용 평가 정보, 다음 실적 예측 등의 데이터가 여기 해당한다.

분석 데이터의 장점은 데이터 자체가 이미 원본 데이터에서 어느 정도의 가공을 통해 정보를 추출해낸 형태라는 점이다. 반면 단점으로는 데이터가 비쌀 수 있고, 데이터 추출 과정에서 bias가 있을 수 있다는 점(게다가 데이터 추출 과정은 공유되지 않을 수 있다), 다른 시장 참여자에게 배타적이지 않을 수 있다는 점이 있다.

Alternative data

대체 데이터는 그 외 거의 모든 데이터에 해당한다. 따라서 데이터가 만들어지는 경로가 매우 다양하고, 주로 비구조화된 형태를 가진다. 여기 해당하는 데이터로는 트위터 같은 SNS부터 위성사진, CCTV 영상, 상품 리뷰 등 다양하다. 너무 다양한 만큼 하나하나의 특성을 깊게 살펴보기보다는 실제 활용 예시를 통해 설명하겠다.

어떻게 보면 이미 딥러닝으로 좋은 성능을 달성한 바 있는 컴퓨터비전, 자연어처리 등의 기술을 직접적으로 적용해볼 수 있는 데이터 종류이기도 하다.

대체 데이터를 분석한 가장 유명한 사례 중 하나는 아마 위성사진일 것 같다. 바로 미국 유통업체인 Walmart의 매출을 예측하기 위한 방법으로, 위성사진을 활용해 각 점포에 주차된 차들을 카운팅했다(기사). 이미 너무 유명해진 사례.

그리고 대체 데이터를 분석하여 투자 시그널을 생성하는 오픈소스 프로젝트도 있다. 직접 코드도 살펴볼 수 있다는 얘기다. 바로 trump2cash라는 이름부터 재밌는 프로젝트다. 트럼프 미국 대통령은 하루에도 몇 번씩 트윗을 올리기로 유명하다. 그리고 실제로 트럼프의 트윗 때문에 시장이 요동친 적도 여러 번 있다. 이 프로젝트는 여기에 착안해서 트럼프의 트윗에서 어떤 회사가 언급되면 sentiment analysis를 해서 투자 시그널을 생성해준다.

그리고 이건 내가 직접 목격했던 상황인데.. 2020년 초, 코로나로 인한 수요 감소와 지속적인 원유 감산 합의 실패로 원유 가격이 엄청나게 떨어지고 한 때 선물 가격이 마이너스까지 갔던 적이 있었다. 그리고 4월 2일, 트럼프가 갑자기 트위터에 “내가 사우디 왕세자랑 방금 통화했는데 러시아랑 감산 합의했대ㅇㅇ”라를 트윗을 올렸고 그 순간 원유 가격이 몇 분 내에 무려 30%까지 급등했다. 직접 보니 변동성이 어마어마하더라.. 이 때 trump2cash를 약간 수정해서 원유 선물에 적용해봤으면 어땠을까 라는 생각도 한 번 해본다. 누군가는 그렇게 해서 짭짤한 수익을 벌었을 수도.

정리

이것저것 쓰다 보니 글이 좀 길어졌다. 그래도 데이터과학쪽 배경지식이 있는 사람이 금융 분야의 도메인 지식을 접하려고 할 때 도움이 될 만한 정보들을 중심으로 웬만큼 정리가 된 것 같다. 물론 여기 나와 있는 데이터가 전부는 아니고, 앞으로 공부를 하면서 추가할 것이 있다면 추가로 업데이트 할 예정이다.

이번 글의 핵심을 정리하자면 다음과 같다.

• 투자가 어려운 이유와 금융 머신러닝에서 유의할 점
  • 금융 데이터는 low signal-to-noise ratio를 가진다.
  • 그리고 금융 시장은 변화하기 때문에 대다수의 관찰 가능한 금융 데이터가 i.i.d를 만족하지 않는다.
  • 그래서 금융에 머신러닝을 잘 적용하려면 전처리나 feature 확보를 통해 signal-to-noise ratio를 높이고 정보 측면에 있어 i.i.d에 가까운 분포를 만들어야 한다.
• 금융 데이터는 생성 과정에 따라 Fundamental data, Market data(시장 데이터), Analytics(분석 데이터), Alternative data(대체 데이터)로 나눌 수 있다.
• 대표적인 시장 데이터인 수익률 데이터의 특성에 대해 자세히 살펴봤다.

다음 글인 <금융 데이터의 종류 (2) - 거래하고자 하는 ‘상품’> 에서는 좀 더 금융 비즈니스 자체에 집중해서 각 상품이 어떤 특징을 가지는지에 대해 써보려고 한다.